MATEMÁTICA III
Faça uma análise do ciclo a seguir,
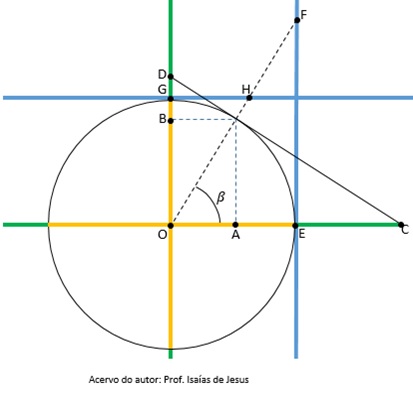
A respeito do estudo feito sobre o ciclo dado podemos afirmar:
%7D%7D%7D%3D%7B%5Coverline%7B%7B%7BO%7D%7BC%7D%7D%7D%7D)
%7D%7D%7D%3D%7B%5Coverline%7B%7B%7BO%7D%7BE%7D%7D%7D%7D)
%7D%7D%7D%7D%7D%3D%7B%5Coverline%7B%7B%7BO%7D%7BD%7D%7D%7D%7D)
%7D%3D%7B%5Coverline%7B%7B%7BO%7D%7BA%7D%7D%7D%7D)
%7D%7D%7D%3D%7B%5Coverline%7B%7B%7BO%7D%7BF%7D%7D%7D%7D)
Sendo cossecx = 7/4, com  , o valor de cosx é exatamente:
, o valor de cosx é exatamente:
 .
.
 .
.
 .
.
 .
.
 .
.
A previsão de exportações mensais de grãos em toneladas de determinada região é dada pela função:
![E(t) = 2.[(200-sec(pi/t)).cossec((pi)/(3/2t))] - 40sen(pit) + 200cos((2pit)/3)](http://sga.uniube.br/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BE%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%3D%7B2%7D.%7B%5Cleft%5B%7B%5Cleft(%7B200%7D-%7B%5Csec%7B%7B%5Cleft(%5Cfrac%7B%5Cpi%7D%7B%7Bt%7D%7D%5Cright)%7D%7D%7D%5Cright)%7D.%7B%5Ccos%7B%7B%5Csec%7B%7B%5Cleft(%5Cfrac%7B%7B%5Cpi%7D%7D%7B%7B%5Cfrac%7B%7B3%7D%7D%7B%7B2%7D%7D%7Bt%7D%7D%7D%5Cright)%7D%7D%7D%7D%7D%5Cright%5D%7D-%7B40%7D%7Bs%7D%7Be%7D%7Bn%7D%7B%5Cleft(%5Cpi%7Bt%7D%5Cright)%7D%2B%7B200%7D%7B%5Ccos%7B%7B%5Cleft(%5Cfrac%7B%7B%7B2%7D%5Cpi%7Bt%7D%7D%7D%7B%7B3%7D%7D%5Cright)%7D%7D%7D) , com
, com  .
.
Considerando t = 1 referente ao mês de janeiro, então a previsão de aproximada de exportações, em toneladas, no mês de dezembro é:
Dados: %7D%5Cstackrel%7B%5Csim%7D%7B%3D%7D%7B0%7D%2C%7B1736%7D) e
e %7D%7D%7D%5Cstackrel%7B%5Csim%7D%7B%3D%7D%7B0%7D%2C%7B9659%7D.)
859,54
1769,85
258,46
2492,19
4789,25
Se  , o valor da expressão
, o valor da expressão %7D%7D%7D.%7B%5Ccot%7B%7B%5Cleft(%7Bx%7D%2B%5Cfrac%7B%5Cpi%7D%7B%7B2%7D%7D%5Cright)%7D%7D%7D%7D%7D%7B%7B%7B%5Ccot%7B%7Bg%7B%7B%5Cleft(%7Bx%7D%5Cright)%7D%7D%7D%7D%7D.%7B%5Ccot%7B%7Bg%7B%7B%5Cleft(%7Bx%7D%2B%5Cpi%5Cright)%7D%7D%7D%7D%7D%7D%7D) é igual a:
é igual a:




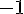
O gráfico a seguir, representa a função:
y = sen(x)
y = cos(x)
y = tg(x)
y = cotg(x)
y = sec(x)
Uma função do tipo y = cosx, tem imagem definida por [-1,1]. Sabemos que a imagem só é alterada por fatores externos ao cosx.
Assim a imagem da função tipo y = a + b.cosx será definida por [a - b, a+b].
De acordo com o contexto, considere a função  . A imagem da função y é dado por:
. A imagem da função y é dado por:
[- 2, 6]
[1, 3]
[2, 4]
[- 4, 4]
[- 1, 1]
Sobre o ciclo abaixo,

http://vestibular.uol.com.br/resumo-das-disciplinas/matematica/trigonometria-do-triangulo-retangulo-e-circulo-trigonometrico.htm
Sobre a função seno e cosseo, e correto afirmar:
No 2° quadrante temos seno > 0 e cosseno > 0
No 1° quadrante temos seno < 0 e cosseno > 0.
No 2° quadrante temos seno > 0 e cosseno < 0.
No 4° quadrante temos seno > 0 e cosseno > 0.
No 3° quadrante temos seno > 0 e cosseno < 0.
A primeira determinação positiva e a expressão geral dos arcos côngruos a 1940 ° são respectivamente:
140° ; 140° + k . 180° , k 
140° ; 140° + k . 360° , k 
90° ; 90° + k . 60° , k 
140° ; 140° + k . 360° , k 
120° ; 120° + k . 180° , k 
Sobre transformações trigonométricas;
I. sen75° = sen30° + sen45°
II. sen 75° = sen30° . sen45° - cos45°.cos30°
III. tg75° = ( tg30° + tg45° ) / ( 1 - tg30° . tg45° )
É correto afirmar:

Sendo cossecx = 7/4, com  , o valor de cosx é exatamente:
, o valor de cosx é exatamente:
 .
.
 .
.
 .
.
 .
.
 .
.
A previsão de exportações mensais de grãos em toneladas de determinada região é dada pela função:
![E(t) = 2.[(200-sec(pi/t)).cossec((pi)/(3/2t))] - 40sen(pit) + 200cos((2pit)/3)](http://sga.uniube.br/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BE%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%3D%7B2%7D.%7B%5Cleft%5B%7B%5Cleft(%7B200%7D-%7B%5Csec%7B%7B%5Cleft(%5Cfrac%7B%5Cpi%7D%7B%7Bt%7D%7D%5Cright)%7D%7D%7D%5Cright)%7D.%7B%5Ccos%7B%7B%5Csec%7B%7B%5Cleft(%5Cfrac%7B%7B%5Cpi%7D%7D%7B%7B%5Cfrac%7B%7B3%7D%7D%7B%7B2%7D%7D%7Bt%7D%7D%7D%5Cright)%7D%7D%7D%7D%7D%5Cright%5D%7D-%7B40%7D%7Bs%7D%7Be%7D%7Bn%7D%7B%5Cleft(%5Cpi%7Bt%7D%5Cright)%7D%2B%7B200%7D%7B%5Ccos%7B%7B%5Cleft(%5Cfrac%7B%7B%7B2%7D%5Cpi%7Bt%7D%7D%7D%7B%7B3%7D%7D%5Cright)%7D%7D%7D) , com
, com  .
.
Considerando t = 1 referente ao mês de janeiro, então a previsão de aproximada de exportações, em toneladas, no mês de dezembro é:
Dados: %7D%5Cstackrel%7B%5Csim%7D%7B%3D%7D%7B0%7D%2C%7B1736%7D) e
e %7D%7D%7D%5Cstackrel%7B%5Csim%7D%7B%3D%7D%7B0%7D%2C%7B9659%7D.)
859,54
1769,85
258,46
2492,19
4789,25
Se  , o valor da expressão
, o valor da expressão %7D%7D%7D.%7B%5Ccot%7B%7B%5Cleft(%7Bx%7D%2B%5Cfrac%7B%5Cpi%7D%7B%7B2%7D%7D%5Cright)%7D%7D%7D%7D%7D%7B%7B%7B%5Ccot%7B%7Bg%7B%7B%5Cleft(%7Bx%7D%5Cright)%7D%7D%7D%7D%7D.%7B%5Ccot%7B%7Bg%7B%7B%5Cleft(%7Bx%7D%2B%5Cpi%5Cright)%7D%7D%7D%7D%7D%7D%7D) é igual a:
é igual a:




O gráfico a seguir, representa a função:

y = sen(x)
y = cos(x)
y = tg(x)
y = cotg(x)
y = sec(x)
Uma função do tipo y = cosx, tem imagem definida por [-1,1]. Sabemos que a imagem só é alterada por fatores externos ao cosx.
Assim a imagem da função tipo y = a + b.cosx será definida por [a - b, a+b].
De acordo com o contexto, considere a função  . A imagem da função y é dado por:
. A imagem da função y é dado por:
[- 2, 6]
[1, 3]
[2, 4]
[- 4, 4]
[- 1, 1]
Sobre o ciclo abaixo,

http://vestibular.uol.com.br/resumo-das-disciplinas/matematica/trigonometria-do-triangulo-retangulo-e-circulo-trigonometrico.htm
Sobre a função seno e cosseo, e correto afirmar:
No 2° quadrante temos seno > 0 e cosseno > 0
No 1° quadrante temos seno < 0 e cosseno > 0.
No 2° quadrante temos seno > 0 e cosseno < 0.
No 4° quadrante temos seno > 0 e cosseno > 0.
No 3° quadrante temos seno > 0 e cosseno < 0.
A primeira determinação positiva e a expressão geral dos arcos côngruos a 1940 ° são respectivamente:
140° ; 140° + k . 180° , k 
140° ; 140° + k . 360° , k 
90° ; 90° + k . 60° , k 
140° ; 140° + k . 360° , k 
120° ; 120° + k . 180° , k 
Sobre transformações trigonométricas;
I. sen75° = sen30° + sen45°
II. sen 75° = sen30° . sen45° - cos45°.cos30°
III. tg75° = ( tg30° + tg45° ) / ( 1 - tg30° . tg45° )
É correto afirmar:
A previsão de exportações mensais de grãos em toneladas de determinada região é dada pela função:
![E(t) = 2.[(200-sec(pi/t)).cossec((pi)/(3/2t))] - 40sen(pit) + 200cos((2pit)/3)](http://sga.uniube.br/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BE%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%3D%7B2%7D.%7B%5Cleft%5B%7B%5Cleft(%7B200%7D-%7B%5Csec%7B%7B%5Cleft(%5Cfrac%7B%5Cpi%7D%7B%7Bt%7D%7D%5Cright)%7D%7D%7D%5Cright)%7D.%7B%5Ccos%7B%7B%5Csec%7B%7B%5Cleft(%5Cfrac%7B%7B%5Cpi%7D%7D%7B%7B%5Cfrac%7B%7B3%7D%7D%7B%7B2%7D%7D%7Bt%7D%7D%7D%5Cright)%7D%7D%7D%7D%7D%5Cright%5D%7D-%7B40%7D%7Bs%7D%7Be%7D%7Bn%7D%7B%5Cleft(%5Cpi%7Bt%7D%5Cright)%7D%2B%7B200%7D%7B%5Ccos%7B%7B%5Cleft(%5Cfrac%7B%7B%7B2%7D%5Cpi%7Bt%7D%7D%7D%7B%7B3%7D%7D%5Cright)%7D%7D%7D) , com
, com  .
.
Considerando t = 1 referente ao mês de janeiro, então a previsão de aproximada de exportações, em toneladas, no mês de dezembro é:
Dados: %7D%5Cstackrel%7B%5Csim%7D%7B%3D%7D%7B0%7D%2C%7B1736%7D) e
e %7D%7D%7D%5Cstackrel%7B%5Csim%7D%7B%3D%7D%7B0%7D%2C%7B9659%7D.)
859,54
1769,85
258,46
2492,19
4789,25
Se  , o valor da expressão
, o valor da expressão %7D%7D%7D.%7B%5Ccot%7B%7B%5Cleft(%7Bx%7D%2B%5Cfrac%7B%5Cpi%7D%7B%7B2%7D%7D%5Cright)%7D%7D%7D%7D%7D%7B%7B%7B%5Ccot%7B%7Bg%7B%7B%5Cleft(%7Bx%7D%5Cright)%7D%7D%7D%7D%7D.%7B%5Ccot%7B%7Bg%7B%7B%5Cleft(%7Bx%7D%2B%5Cpi%5Cright)%7D%7D%7D%7D%7D%7D%7D) é igual a:
é igual a:




O gráfico a seguir, representa a função:

y = sen(x)
y = cos(x)
y = tg(x)
y = cotg(x)
y = sec(x)
Uma função do tipo y = cosx, tem imagem definida por [-1,1]. Sabemos que a imagem só é alterada por fatores externos ao cosx.
Assim a imagem da função tipo y = a + b.cosx será definida por [a - b, a+b].
De acordo com o contexto, considere a função  . A imagem da função y é dado por:
. A imagem da função y é dado por:
[- 2, 6]
[1, 3]
[2, 4]
[- 4, 4]
[- 1, 1]
Sobre o ciclo abaixo,

http://vestibular.uol.com.br/resumo-das-disciplinas/matematica/trigonometria-do-triangulo-retangulo-e-circulo-trigonometrico.htm
Sobre a função seno e cosseo, e correto afirmar:
No 2° quadrante temos seno > 0 e cosseno > 0
No 1° quadrante temos seno < 0 e cosseno > 0.
No 2° quadrante temos seno > 0 e cosseno < 0.
No 4° quadrante temos seno > 0 e cosseno > 0.
No 3° quadrante temos seno > 0 e cosseno < 0.
A primeira determinação positiva e a expressão geral dos arcos côngruos a 1940 ° são respectivamente:
140° ; 140° + k . 180° , k 
140° ; 140° + k . 360° , k 
90° ; 90° + k . 60° , k 
140° ; 140° + k . 360° , k 
120° ; 120° + k . 180° , k 
Sobre transformações trigonométricas;
I. sen75° = sen30° + sen45°
II. sen 75° = sen30° . sen45° - cos45°.cos30°
III. tg75° = ( tg30° + tg45° ) / ( 1 - tg30° . tg45° )
É correto afirmar:
859,54
1769,85
258,46
2492,19
4789,25
Se  , o valor da expressão
, o valor da expressão %7D%7D%7D.%7B%5Ccot%7B%7B%5Cleft(%7Bx%7D%2B%5Cfrac%7B%5Cpi%7D%7B%7B2%7D%7D%5Cright)%7D%7D%7D%7D%7D%7B%7B%7B%5Ccot%7B%7Bg%7B%7B%5Cleft(%7Bx%7D%5Cright)%7D%7D%7D%7D%7D.%7B%5Ccot%7B%7Bg%7B%7B%5Cleft(%7Bx%7D%2B%5Cpi%5Cright)%7D%7D%7D%7D%7D%7D%7D) é igual a:
é igual a:




O gráfico a seguir, representa a função:

y = sen(x)
y = cos(x)
y = tg(x)
y = cotg(x)
y = sec(x)
Uma função do tipo y = cosx, tem imagem definida por [-1,1]. Sabemos que a imagem só é alterada por fatores externos ao cosx.
Assim a imagem da função tipo y = a + b.cosx será definida por [a - b, a+b].
De acordo com o contexto, considere a função  . A imagem da função y é dado por:
. A imagem da função y é dado por:
[- 2, 6]
[1, 3]
[2, 4]
[- 4, 4]
[- 1, 1]
Sobre o ciclo abaixo,

http://vestibular.uol.com.br/resumo-das-disciplinas/matematica/trigonometria-do-triangulo-retangulo-e-circulo-trigonometrico.htm
Sobre a função seno e cosseo, e correto afirmar:
No 2° quadrante temos seno > 0 e cosseno > 0
No 1° quadrante temos seno < 0 e cosseno > 0.
No 2° quadrante temos seno > 0 e cosseno < 0.
No 4° quadrante temos seno > 0 e cosseno > 0.
No 3° quadrante temos seno > 0 e cosseno < 0.
A primeira determinação positiva e a expressão geral dos arcos côngruos a 1940 ° são respectivamente:
140° ; 140° + k . 180° , k 
140° ; 140° + k . 360° , k 
90° ; 90° + k . 60° , k 
140° ; 140° + k . 360° , k 
120° ; 120° + k . 180° , k 
Sobre transformações trigonométricas;
I. sen75° = sen30° + sen45°
II. sen 75° = sen30° . sen45° - cos45°.cos30°
III. tg75° = ( tg30° + tg45° ) / ( 1 - tg30° . tg45° )
É correto afirmar:
O gráfico a seguir, representa a função:

y = sen(x)
y = cos(x)
y = tg(x)
y = cotg(x)
y = sec(x)
Uma função do tipo y = cosx, tem imagem definida por [-1,1]. Sabemos que a imagem só é alterada por fatores externos ao cosx.
Assim a imagem da função tipo y = a + b.cosx será definida por [a - b, a+b].
De acordo com o contexto, considere a função  . A imagem da função y é dado por:
. A imagem da função y é dado por:
[- 2, 6]
[1, 3]
[2, 4]
[- 4, 4]
[- 1, 1]
Sobre o ciclo abaixo,

http://vestibular.uol.com.br/resumo-das-disciplinas/matematica/trigonometria-do-triangulo-retangulo-e-circulo-trigonometrico.htm
Sobre a função seno e cosseo, e correto afirmar:
No 2° quadrante temos seno > 0 e cosseno > 0
No 1° quadrante temos seno < 0 e cosseno > 0.
No 2° quadrante temos seno > 0 e cosseno < 0.
No 4° quadrante temos seno > 0 e cosseno > 0.
No 3° quadrante temos seno > 0 e cosseno < 0.
A primeira determinação positiva e a expressão geral dos arcos côngruos a 1940 ° são respectivamente:
140° ; 140° + k . 180° , k 
140° ; 140° + k . 360° , k 
90° ; 90° + k . 60° , k 
140° ; 140° + k . 360° , k 
120° ; 120° + k . 180° , k 
Sobre transformações trigonométricas;
I. sen75° = sen30° + sen45°
II. sen 75° = sen30° . sen45° - cos45°.cos30°
III. tg75° = ( tg30° + tg45° ) / ( 1 - tg30° . tg45° )
É correto afirmar:

y = sen(x)
y = cos(x)
y = tg(x)
y = cotg(x)
y = sec(x)
Uma função do tipo y = cosx, tem imagem definida por [-1,1]. Sabemos que a imagem só é alterada por fatores externos ao cosx.
Assim a imagem da função tipo y = a + b.cosx será definida por [a - b, a+b].
De acordo com o contexto, considere a função  . A imagem da função y é dado por:
. A imagem da função y é dado por:
[- 2, 6]
[1, 3]
[2, 4]
[- 4, 4]
[- 1, 1]
Sobre o ciclo abaixo,

http://vestibular.uol.com.br/resumo-das-disciplinas/matematica/trigonometria-do-triangulo-retangulo-e-circulo-trigonometrico.htm
Sobre a função seno e cosseo, e correto afirmar:
No 2° quadrante temos seno > 0 e cosseno > 0
No 1° quadrante temos seno < 0 e cosseno > 0.
No 2° quadrante temos seno > 0 e cosseno < 0.
No 4° quadrante temos seno > 0 e cosseno > 0.
No 3° quadrante temos seno > 0 e cosseno < 0.
A primeira determinação positiva e a expressão geral dos arcos côngruos a 1940 ° são respectivamente:
140° ; 140° + k . 180° , k 
140° ; 140° + k . 360° , k 
90° ; 90° + k . 60° , k 
140° ; 140° + k . 360° , k 
120° ; 120° + k . 180° , k 
Sobre transformações trigonométricas;
I. sen75° = sen30° + sen45°
II. sen 75° = sen30° . sen45° - cos45°.cos30°
III. tg75° = ( tg30° + tg45° ) / ( 1 - tg30° . tg45° )
É correto afirmar:
[- 2, 6]
[1, 3]
[2, 4]
[- 4, 4]
[- 1, 1]
Sobre o ciclo abaixo,

http://vestibular.uol.com.br/resumo-das-disciplinas/matematica/trigonometria-do-triangulo-retangulo-e-circulo-trigonometrico.htm
Sobre a função seno e cosseo, e correto afirmar:
No 2° quadrante temos seno > 0 e cosseno > 0
No 1° quadrante temos seno < 0 e cosseno > 0.
No 2° quadrante temos seno > 0 e cosseno < 0.
No 4° quadrante temos seno > 0 e cosseno > 0.
No 3° quadrante temos seno > 0 e cosseno < 0.
A primeira determinação positiva e a expressão geral dos arcos côngruos a 1940 ° são respectivamente:
140° ; 140° + k . 180° , k 
140° ; 140° + k . 360° , k 
90° ; 90° + k . 60° , k 
140° ; 140° + k . 360° , k 
120° ; 120° + k . 180° , k 
Sobre transformações trigonométricas;
I. sen75° = sen30° + sen45°
II. sen 75° = sen30° . sen45° - cos45°.cos30°
III. tg75° = ( tg30° + tg45° ) / ( 1 - tg30° . tg45° )
É correto afirmar:

No 2° quadrante temos seno > 0 e cosseno > 0
No 1° quadrante temos seno < 0 e cosseno > 0.
No 2° quadrante temos seno > 0 e cosseno < 0.
No 4° quadrante temos seno > 0 e cosseno > 0.
No 3° quadrante temos seno > 0 e cosseno < 0.
A primeira determinação positiva e a expressão geral dos arcos côngruos a 1940 ° são respectivamente:
140° ; 140° + k . 180° , k 
140° ; 140° + k . 360° , k 
90° ; 90° + k . 60° , k 
140° ; 140° + k . 360° , k 
120° ; 120° + k . 180° , k 
Sobre transformações trigonométricas;
I. sen75° = sen30° + sen45°
II. sen 75° = sen30° . sen45° - cos45°.cos30°
III. tg75° = ( tg30° + tg45° ) / ( 1 - tg30° . tg45° )
É correto afirmar:
140° ; 140° + k . 180° , k
140° ; 140° + k . 360° , k
90° ; 90° + k . 60° , k
140° ; 140° + k . 360° , k
120° ; 120° + k . 180° , k